Benutzer Diskussion:KatrinPapke1

GRENZKOSTEN

Auch als Mehrkosten, proportionale Kosten bezeichnet.

Einführung und Definitíon

Eine immer wieder präsente Frage in vielen Unternehmen ist: „ Um wieviel steigen meine Kosten, wenn ich eine Einheit mehr produziere?“ Um diese Frage beantworten zu können, muss der Begriff der GRENZKOSTEN zunächst näher bestimmt werden.

Grenzkosten in einem Unternehmen beschreiben die Kostenänderung, die durch die Vergrößerung der Produktionsmenge um eine zusätzliche Leistungseinheit eines Produktes entstehen. Diese Mehr- oder Minderkosten beziehen sich stets darauf, dass die Herstellung der zusätzlichen Produktionseinheit innerhalb der vorliegenden Kapazitätstufe erfolgt, d. h. noch freie Kapazität vorliegend ist und somit keine sprungfixen Kosten anfallen. Mathematisch betrachtet, versteht man unter Grenzkosten die erste Ableitung der Kostenfunktion, d. h. die Gesamtkostenfunktion ist nach der Menge zu differenzieren.

Alternative Definitionen

"Grenzkosten sind der Kostenzuwachs, der durch die Mehrproduktion einer Ausbringungseinheit entsteht."

Abzugrenzen ist hierbei jedoch der Begriff der sogenannten sprungfixen Kosten, da die obige Definition nur genau solange ihre Richtigkeit behält, wie die zusätzliche Produktionseinheit innerhalb einer Kapazitätsstufe erstellt werden kann. Voraussetzung hierfür ist, dass in der Kapazitätsstufe, in der sich eine Unternehmung momentan befindet (z. B. vorhandene(s) Maschinen, Anlagen, Produktionshallen) auch noch freie Kapazität vorhanden ist. Ist diese Voraussetzung nicht erfüllt, so müssen zwangsläufig sprungfixe Kosten anfallen, da für die Produktion einer zusätzlichen Leistungseinheit neue Kapazitäten geschaffen werden müssen in Form von Investitionen. Definitionsgemäß versteht man darunter: „Die sprungfixen Kosten sind die Kosten, die bei Überschreiten einer Kapazitätsstufe zusätzlich zu den absolut fixen Kosten der jeweils vorherigen Kapazitätsstufe entstehen und in der neuen Kapazitätsstufe unabhängig vom Beschäftigungsgrad anfallen.“1

„Grafisch betrachtet sind die Grenzkosten die Steigung der Tangente der Gesamtkostenkurve für die untersuchte Ausbringungsmenge.“2 Auch diese Definiton deckt nur einen Teil der notwendigen Erläuterungsbestandteile der Grenzkosten. Sprungfixe Kosten spielen bei Grenzkosten, wie bereits oben eräutert, stets eine wichtige Rolle und sind auch grafisch gut nachvollziehbar. Weiterhin ist auch auf den Fixkostenblock jeder Unternehmung in die Diskussion einzubeziehen, um den Schnittpunkt der Kostenfunktion mit der Ordinate zu ermitteln und sich den Verlauf der Kosten- als auch der Grenzkostenfunktion vorstellen zu können.

Grenzkostenfunktion

Die Grenzkostenfunktion stellt grafisch die erste Ableitung der Kostenfunktion dar. Diese wird im Folgenden, angewandt auf zwei verschiedene Funktionstypen, näher erläutert . Auf der Abszisse wird dabei immer die Ausbringungsmenge x abgetragen und auf der Ordinate die dazugehörigen Gesamtkosten C.

linearer Kostenverlauf

Um zunächst das Prinzip der Grenzkosten darzustellen, wird im Folgenden der lineare Kostenverlauf anhand eines Beispiels erläutert, auch wenn dieser in der Praxis so gut wie nie in reiner Form vorkommt. Die Gesamtkosten[1] ergeben sich aus der Summe von fixen Kosten FC und variablen Kosten VK, wobei letztere mit der Ausbringungsmenge x multipliziert werden.

Linearer Kostenverlauf

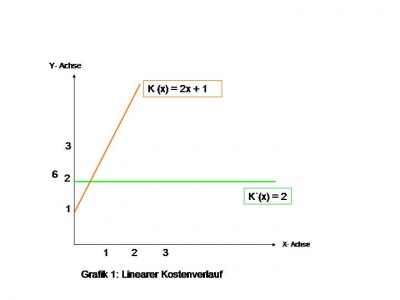
Die Grafik 1 stellt eine lineare Kostenfunktion(blau) dar mit der allgemeinen Form: C = FC + VK*x In unserem Beispiel lautet die Kostenfunktion C = 3€ + 4€*x, d. h. die Fixkosten[2] betragen 3€ und die sich mit der Ausbringungsmenge ändernten variablen Kosten[3] entsprechen 4€. Diese wird blau als Graph dargestellt mit einem Schnittpunkt mit der y- Achse im Punkt (0;3€) und einem positiven Anstieg von 4€. Um die für uns wichtigen Grenzkosten zu ermitteln, muss man die mathematische Definiton der Grenzkosten praktisch umsetzen und die Kostenfunktion C nach x differenzieren. Somit ergibt sich als erste Ableitung

C´= ▲C/▲x

C´= 4€

Die Grenzkostenfunktion (rosa dargestellt) ist unabhängig von der Ausbringungsmenge x und stellt sich als Gerade parallel zur Abszisse verlaufend dar. Dieser lineare Kostenverlauf stellt auch schon einen Sonderfall der Grenzkosten dar, da hier die Grenzkosten GK gleich den variablen Kosten VK sind. Steigt die Produktion in diesem Unternehmen um eine Leistungseinheit, so steigen die Kosten um 4€ unter den Voraussetzungen, die in Abschnitt 1 erläutert wurden. C Gesamtkostenfunktion x Ausbringungsmenge FC fixe Kostenbestandteile VK variable Kostenbestandteile

nicht-linearer Kostenverlauf

Der nicht-lineare Kostenverlauf beruht auf der ertragsgesetzlichen Kostenfunktion und hat bei weitem mehr praktische Relevanz als der lineare Kostenverlauf (siehe a), da er die betrieblich anfallenden Kosten realistischer dargestellt.

Quelle: [4]

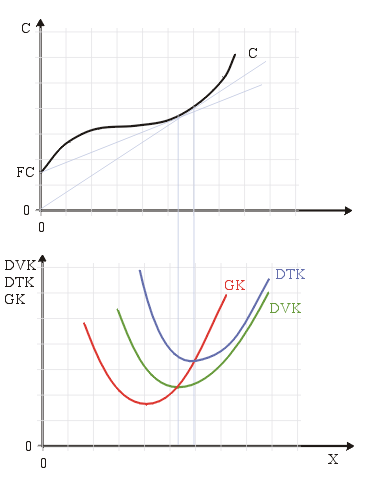
Die Grafik 2 veranschaulicht im oberen Abschnitt den Verlauf der Kostenfunktion, die wie zu erkennen ist, nicht linear,d. h. nicht als Gerade interpretiert werden kann. Im unteren Abschnitt werden die sich aus der Kostenfunktion ergebenden durchschnittlichen variablen Kosten DVK(grüner Graph), durchschnittlichen gesamten Kosten DTK(blauer Graph) und die Grenzkosten GK(roter Graph), die im Folgenden weiter analysiert werden, als eigenständige Funktionen dargestellt. Im Betrieb geht man meist von sinkenden Grenzkosten aus, da sich die Herstellung von großen Mengeneinheiten für ein Unternehmen mehr rentiert als die Produktion von kleinen Mengen. Gründe hierfür sind Skaleneffekte[5] und LernkurveneffekteDer erste Abschnitt der Grenzkostenkurve bis zum Minimum der GK-Funktion verläuft daher zunächst fallend, d. h. mit steigender Ausbringungsmenge sinkt der Preis der jeweils zusätzlich produzierten Leistungseinheit. Hier sind die Grenzkosten kleiner als die durchschnittlichen gesamten Kosten DTK und die Skalenerträge nehmen zu. Es ist also möglich, den doppelten Output zu erreichen ohne dafür die doppelten Kosten zu verursachen. Dann erreicht die Grenzkostenfunktion ihr Minimum im Wendepunkt der Kostenfunktion C und die Grenzkosten steigen wieder an, die Grenzkosten sind jetzt größer als die durchschnittlichen gesamten Kosten DTK und die Skalenerträge nehmen ab, d.h. Mit doppeltem Kosteneinsatz kann nicht der doppelte Absatz eeicht werden. Ursachen für diesen Verlauf sind mit Hilfe der ertragsgesetzlichen Produktions- bzw. Kostenfunktion[6] nachzuvollziehen. Die Grenzkostenfunktion schneidet die Durchschnittskostenfunktionen in deren Minima.

Durchschnitts- und Grenzkostenverläufe bei ertragsgesetzlicher Kostenfunktion Die Grenzkostenstimmen mit den Durchschnittskosten in deren jeweiligen Minima überein.

Anwendung der Grenzkosten ---->GEWINNMAXIMIERUNG

Der Sektor der Unternehmen in ökonomischer Sicht hat immer das Ziel seine Gewinne zu maximieren, d. h. allen Unternehmen wird unterstellt, sie seien Gewinnmaximierer. Der Gewinn G[7] ergibt sich aus der Differenz von Gesamterlösen und den Gesamtkosten.

G = R - C

„Zur Gewinnmaximierung wählt ein Unternehmen den Output, bei dem die Differenz zwischen dem Erlös und den Kosten am größten ist.“3 Grenzerlös R´= Grenzkosten K´

Um dieses Ziel zu erreichen, muss ein Unternehmer vorallem bei seiner Kosten- und der damit verbundenen Preiskalkulation in Abhängigkeit seiner Marktform [8] gut unterrichtet sein.

Gewinnmaximierung im Wettbewerbsunternehmen

Im ersten Fall wird die Marktform eines Polypols[9] unterstellt, d. h. es herrscht vollkommene Konkurrenz zwischen den Unternehmen. Alle Wettbewerbsunternehmen sind der Nachfrage anderer Wirtschaftssektoren und auch des eigenen gleichermaßen ausgesetzt und somit gilt der Peis für ein Produkt als fix und der erzielbare Erlös aus einer zusätzlichen verkauften Leistungseinheit (= Grenzerlös GE)[10] entspricht dem Preis p, den ein Wirtschaftssubjekt für das Produkt zu zahlen hat. Es gilt für alle Wettbewerbsunternehmen: GK = GE = p als Gewinnmaximierungsbedingung. Da der Preis, wie schon erläutert, als konstant angesehen wird, kann ein Polypolist die Gewinnmaximierung nur über die Absatzmenge regeln und nicht über den Preis.

Gewinnmaximierung im Monopol

Anders als der Polypolist kann der Monopolist[11] aufgrund seiner starken Marktpsition als einziger Käufer/Verkäufer seinen Gewinn auch über den Preis bestimmen. Er bestimmt den Schnittpunkt zwischen der Grenzerlöskurve und der Grenzkostenkurve und erhält dabei eine gewinnmaximierende Absatzmenge. Anhand der Nachfragefunktion kann der Momopolist den dazugehörigen Preis festlegen. Produziert der Monopolist unter den errechneten gewinnmaximierenden Menge, so hat er zwar weniger Kosten, aber die entgehenden Erlöse aus den zusätzlichen Verkäufen sind größer als die Kosten und führen somit zu Gewinnminderungen. Stellt der Monopolist im Gegensatz dazu mehr als die gewinnmaximierende Produktionsmenge her, so entstehen ihm einerseits höhere Erlöse, andererseits übersteigen die Kosten für die zusätzliche Produktion über der Gleichgewichtsmenge die Erlöse und führen ebenfalls zur Gewinnschrumpfung. Es gilt die Gewinnmaximerungsbedingung: Grenzerlös R´= Grenzkosten K´

Quellennachweise

Einzelnachweise:

1 http://www.wirtschaftslexikon24.net/suche/search.php?query=sprungfixe+kosten&search=1

2 Rechnungswesen und Controling; Bausteine des Rechnungswesens und ihre Verknüpfungen; Verlag neue Wirtschaftsbriefe (NWB),Herne/Berlin; 1998; S. 272

3 Pindyck, Robert S.,Rubinfeld, Daniel L., Mikroökonomie, 6. Auflage, MünchenS. 361

Literaturnachweise:

Luger, Adolf E., Allgemeine Betriebswirtschaftslehre,Band 1: Der Aufbau des Betriebes,5. Auflage,Carl Hanser Verlag München Wien

Arnold, Botta,Hoefner, Pech, Rechnungswesen und Controlling,Bausteine des Rechnungswesens und ihre Verknüpfungen, Verlag Neue Wirtschaftsbriefe Herne Berlin

Pindyck, Robert S.,Rubinfeld, Daniel L., Mikroökonomie, 6. Auflage, München

Weblinks:

http://www.controllingportal.de/Fachinfo/Kostenrechnung/Grenzkosten.html

http://www.wirtschaftslexikon24.net/d/grenzkosten/grenzkosten.htm

http://www.mikrooekonomie.de/an/kf/ankfdg.htm

Siehe auch

MONOPOL

POLYPOL

ERTRAGSGESETZ

GRENZERLÖS

moin, nutze bitte mal icq zur kontaktaufnahme, danke --Jan eissfeldt 20:20, 25. Apr. 2008 (CEST)

moin

das ist nicht nervig, wir freuen uns aufrichtig über euer engagement. ich hatte dich nur aus der eingangskontrolle gefischt, weil die von dir erstellte seite kommentarlos geleert hattest. ich habe RacoonyRE ist informiert, dass ihr ein projekt macht, aber dass sah für ihn schon sehr nach vandalismus aus.

sämmtliche probleme mit dem artikel kannst du dort besprechen. bitte beachte die hinweise dort und in der reviewdiskussion (weitgehend deckungsgleich).

alternativ zu icq kann ich noch mail, msn und studivz anbieten, gruß --Jan eissfeldt 15:34, 26. Apr. 2008 (CEST)

wir versuchen gerade kapazität freizuschaufeln, ich bitte um gedult und das die diskussion entweder hier oder bei mir sattfindet, ich schlage hier vor, gruß --Jan eissfeldt 20:26, 27. Apr. 2008 (CEST)

siehe bitte auf meine benutzerseite hier im wiwiwiki, gruß --Jan eissfeldt 20:37, 27. Apr. 2008 (CEST)